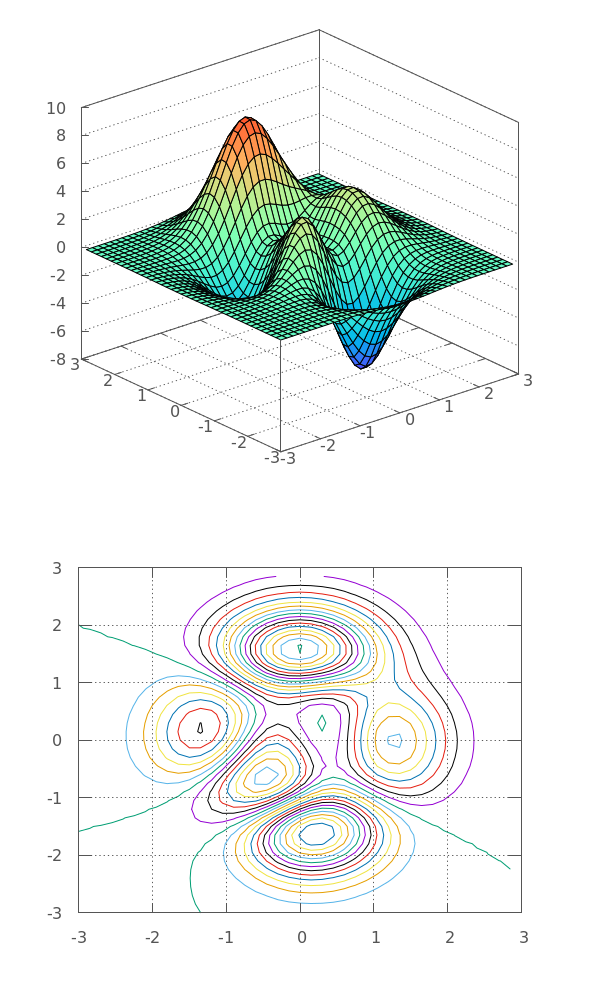
Matlab Peaks¶
Code
// we use make_data_block() helper function provided
// by G3P to turn our vector into a datablock
auto peaks = make_data_block(gp, grid, 3, 40);
// now we can use it in a multiplot
// NOTE: we mix and match C and C++ conventions here...
gp ("set term pngcairo size 600,1000") // make some space for the 2nd plot
("set multiplot layout 2,1 spacing 0,0") // switch to multiplot
<< "splot" // start plotting as the rest has been already set
<< peaks // <-- using peaks once
<< "with pm3d\n";
gp ("set view map")
("set contour")
("set cntrparam levels 50")
("unset surface")
<< "splot"
<< peaks // <-- using peaks twice
<< "w lines\n"
<< "unset multiplot\n"Output


G3P Logo¶
Here’s G3P logo plotted with G3P! 😀
Code
std::vector<float>
g //x y z
{ 1, 1, 1
, 8.3, 1, 1
, 8.3, 1, 9
, 1, 1, 9
, 1, 1, 4.5
, 8.3, 1, 4.5
}
, e //x y z
{ 1, 2.5, 9
, 1, 9, 9
, 4.5, 9, 9
, 4.5, 2.5, 9
, 4.5, 9, 9
, 8, 9, 9
, 8, 2.5, 9
}
, p //x y z
{ 9.3, 1, 1
, 9.3, 1, 9
, 9.3, 9, 9
, 9.3, 9, 4.5
, 9.3, 1, 4.5
}
;
auto lg = make_data_block(gp, g, 3);
auto l3 = make_data_block(gp, e, 3);
auto lp = make_data_block(gp, p, 3);
gp << "set view 55,44,0.9,1.72\n"
<< "set border linecolor 'grey'\n"
<< "set border 895-32\n"
<< "set xrange [0:10]\n"
<< "set yrange [0:10]\n"
<< "set zrange [0:10]\n"
<< "set grid x y z\n"
<< "unset key\n"
<< "set style line 1 lt rgb 'red' lw 20\n"
<< "set style line 2 lt rgb 'green' lw 20\n"
<< "set style line 3 lt rgb 'blue' lw 20\n"
<< "set ticslevel 0\n"
<< "set format x ''; set format y ''; set format z ''\n"
;
gp << "splot"
<< lg << "u 1:2:3 w l ls 1,"
<< l3 << "u 1:2:3 w l ls 2,"
<< lp << "u 1:2:3 w l ls 3"
<< g3p::endlOutput


Bessel animation¶
A nice animation from gnuplotting.org
Code
g3p::gnuplot gp;
gp ( "set term gif enhanced transparent animate" )
( "set palette rgb 3,9,9" )
( "unset key; unset colorbox; unset border; unset tics" )
( "set lmargin at screen 0.03" )
( "set bmargin at screen 0" )
( "set rmargin at screen 0.97" )
( "set tmargin at screen 1" )
( "set parametric" )
// Bessel function, which is moving in time
( "bessel(x,t) = besj0(x) * cos(2*pi*t)" )
// calculate the zeros for the bessel function (see Watson,
// "A Treatise on the heory of Bessel Functions", 1966, page 505)
( "n = 6 # number of zeros" )
( "k = (n*pi-1.0/4*pi)" )
( "u_0 = k + 1/(8*k) - 31/(384*k)**3 + 3779/(15360*k)**5" )
( "set urange [0:u_0]" )
( "set vrange[0:1.5*pi]" )
( "set cbrange [-1:1]" )
( "set zrange[-1:1]" )
( "set isosamples 200,100" )
( "set pm3d depthorder" )
( "set view 40,200" )
;
for (float t = 0; t < 2; t += 0.02)
gp ( "splot u*sin(v),u*cos(v),bessel(u,%f) w pm3d ls 1", t);
gp ("unset output")Output
